高斯变量之外不存在标准差,即使存在,也无关紧要,并且说明不了什么。但事情却变得更糟了。高斯变量家族(有许多朋友和亲戚,比如泊松分布)是唯一能用标准差(以及平均值)描述的分布。你不再需要别的东西了。钟形曲线满足了那些容易上当的人对简化论的需求。
如果你在大学上过(无聊的)统计课,不明白教授为什么兴奋,不知道“标准差”是什么意思,不要担心。标准差的概念在平均斯坦以外毫无意义。假如你上过审美神经生物学或者殖民地时期之后的非洲舞蹈课程,这显然对你更有好处,也更具娱乐性。从经验主义的角度,这一点很容易看出来。
还有一些在高斯世界之外没有意义或没有重大意义的概念:相关性,以及(更糟糕的)回归。它们在我们的方法中根深蒂固,在商业谈话中不听到“相关性”这个词是很难的。
爱上确定性
要想了解相关性在平均斯坦以外多么没有意义,只需要看一看涉及两个极端斯坦变量的历史序列,比如债券和股市,两只股票的价格,或者美国儿童图书销量变化和中国化肥产量,又或者纽约房地产价格和蒙古股市收益率。计算这些成对变量在不同子期间的相关性,比如1994年、1995年、1996年,等等。计算结果很可能表现出严重的不稳定性,它取决于计算的期间。但人们谈论相关性时仿佛它是某种真实确定的东西,人们倾向于把它实际化、具体化,并赋予它物理属性。
其结果就是,对高斯变量平均值的偏离,或者说“误差”,不会造成麻烦。它们很小,可以忽略。它们只会在平均值附近引起温和的波动。
同样的具体性假象也会影响所谓的“标准”差。选取任何价格或价值的历史序列,将之分割为子序列,计算“标准”差。奇怪吗?每个子序列会有一个不同的“标准”差。那为什么人们还要谈标准差呢?想想吧。
上面的例子就是平均斯坦最高法则的应用:当你有大量赌徒时,单个赌徒对总体只可能造成微小的影响。
请注意,正如叙述谬误一样,当你拿过去数据计算出单一的相关性或标准差时,你忽略了它们的不稳定性。
赌场经营者非常明白这一点,这就是他们从不亏本的原因(如果经营得当的话)。他们不让赌徒下大注,而喜欢让许多赌徒下很多受限制的小注。赌徒的总赌注可能有2000万美元,但你不需要为赌场担心:每注平均可能只有20美元;赌场对最大赌注设了上限,赌场老板因此晚上可以安心睡觉。所以赌场收入的变化会小到可笑的地步,不管总赌注有多大。你永远不会看到谁带着10亿美元离开赌场,在宇宙的整个历史中都看不到。
怎样制造灾难
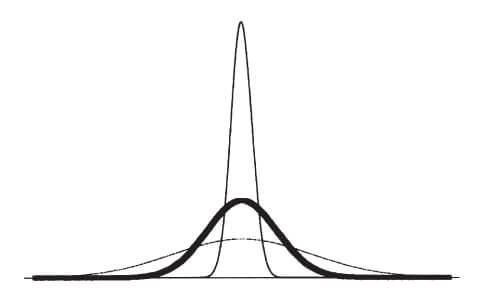
注:在平均斯坦,随着样本规模的增大,被观测到的平均值越来越稳定,在图中可以看到,曲线越来越窄。这就是一切统计理论的工作原理(或者所谓的工作原理)。平均斯坦的不确定性在平均化之下消失了。这就是人们常说的“大数定理”。
如果你使用“统计显著性”这种说法,请小心它所带来的确定性假象。人们有可能把观测误差按照满足高斯分布的条件处理,而这要求它必须来自高斯环境,比如平均斯坦。
图15–2 大数定理的原理
为了看清高斯方法的误用多么普遍以及危害多么大,请看一部由多产作家、大法官理查德·波斯纳(Richard Posner)撰写的(无聊的)书《大灾难》(Catastrophe)。波斯纳哀叹公务员对随机性的误解,建议政府的政策制定者向经济学家学习统计学。法官波斯纳看上去正在努力制造灾难。尽管属于应该多花时间读书而不是写书的人,他还是有可能成为具有洞察力的、深刻的、原创的思想家。和许多人一样,他只是不知道平均斯坦和极端斯坦的区别,他相信统计学是“科学”,而不是骗局。假如你碰到他,请告诉他真相。
凯特勒的平均怪兽
安全的咖啡杯演示了高斯变量的随机性是可以通过平均来消除的。如果我的咖啡杯是一个大粒子,或者能够表现为一个大粒子,那么它的跳跃就是一个问题。但我的杯子是由数万亿非常小的粒子组成的整体。
这种叫作高斯钟形曲线的怪兽并不是高斯的杰作,虽然他对此做了研究,但他是进行理论研究的数学家,而没有像那些统计科学家一样对现实的构造发表言论。G.H.哈迪(G.H.Hardy)在《数学家的歉意》一文中写道:
但从物理上讲,我的咖啡杯是可能跳跃的,这是非常低的可能性,但仍是可能的。粒子一直在跳跃。但为什么由跳跃的粒子组成的咖啡杯本身不跳呢?原因很简单,要让杯子跳起来,所有粒子必须向同一个方向跳跃,并且连续这样同步跳几次(同时导致桌子向相反方向移动)。我的咖啡杯的数万亿粒子不可能同时向一个方向跳;在宇宙的整个历史中这种情况也不会发生一次。所以我可以安全地把咖啡杯放在写字台的边缘,去操心更严重的不确定性来源。
“真正的”数学家的“真正的”数学,比如费马(Fermat)、欧拉(Euler)、高斯、阿贝尔(Abel)和黎曼(Riemann)的数学,是完全“无用”的(“应用”数学和“纯”数学都是如此)。
我一生中喝过许多杯咖啡(它是我最上瘾的东西)。我从未遇到杯子从桌上跳起两英尺的情况,咖啡也从来没有自动从杯子里流到这份书稿上。要想发生这类情况,需要的可不仅仅是对咖啡上瘾。它可能需要超过人们想象的时间才会发生,概率太小了,是1后面加上许多零分之一,我用全部的业余时间可能都写不完这个数字。
我之前提到过,钟形曲线是由一个赌徒编造的,他就是亚伯拉罕·棣莫弗(Abraham de Moivre,1667—1754),一个法国加尔文派的避难者,他一生中大部分时间生活在伦敦,说着口音浓重的英语。但凯特勒才是思想史上最具破坏性的人,而不是高斯。
第三章对平均斯坦的讨论中提到,个体不可能对总体产生影响。随着总体规模的增加,这一特点越来越强。平均值会越来越稳定,所有样本都是相似的。
阿道夫·凯特勒(Adolphe Quételet,1796—1874)提出了体质平均人的概念。凯特勒本人一点也不平均,他是“一个极具创造激情的人,一个精力充沛、具有创造力的人”。他写诗,甚至与人合写了一部歌剧。凯特勒的根本问题在于,他是一个数学家,而不是经验主义科学家,但他不知道这一点。他在钟形曲线中发现了和谐。
咖啡杯会跳起来吗
问题有两个层面。首先,凯特勒有一种标准化思维,他想把世界塞入他的平均理论中,从这个意义上讲,平均对他而言是“常规”。能够不考虑非常规的、“不规范的”情况以及黑天鹅事件对总体的影响是一件不错的事,但把这个梦留给乌托邦吧。
让我为你展示高斯钟形曲线是如何把随机性从生活中抹去的,这正是它流行的原因。我们喜欢它,因为它带来了确定性!怎么做到的呢?通过平均化,我将在下面讨论。
其次,存在一个严重的经验问题。凯特勒把钟形曲线应用于一切地方。他被钟形曲线遮住了眼睛,这让我再次看到,一旦你让钟形曲线进入你的头脑,就很难把它赶出来。后来,弗兰克·伊西德罗·埃奇沃思(Frank Ysidro Edgeworth)把这种将钟形曲线用在一切地方的严重错误称为凯特勒错误。
请再次注意如下原则:事件越稀有,我们对其概率估计的错误越大,即使使用高斯方法。
金色的平均主义
更专业的说法是,如果存在巨人和侏儒,二者之间的差异达到几个数量级,你仍然可能处于平均斯坦。为什么?假设你以1000个人为样本,其中既包含侏儒也包含巨人。你可能会在样本中看到许多巨人,而不是极少数巨人。你的平均值不会受到额外增加的一个巨人的影响,因为你预期到巨人是样本的一部分,所以你的平均值会比较大。也就是说,最大观测值不会偏离平均值太远。平均值总会涵盖两类人——巨人与侏儒,所以两者都不会太罕见,你只有在极少数情况下才会遇到超级巨人或超小侏儒,这种情况是一个偏离单位较大的平均斯坦。
凯特勒为同时代的理想主义者提供了他们所渴望的产品。这个后启蒙时代的每一个人都渴望金色平均主义:财富、身高、体重等等。这种渴望包含着一种愿望的因素,再加上和谐以及……柏拉图化。
请注意,我并不是在告诉你平均斯坦的随机性不会产生某种极端情况,而是说它们很少发生,加起来也不会有重大影响。这些极端情况的影响小得可怜,而且随着总体的增大而下降。
我总是记得我父亲的告诫,“美德在于适度”。很长一段时间,那就是理想。从这种意义上讲,平均甚至被认为是金色的,所有人都拥抱平均主义。
处理最大值不会与平均值相差太大的变量时,高斯方法对我们很有用。如果数量受到向下的拉力,或者如果存在物理上限,使得非常大的数值不会出现,那么我们在平均斯坦。如果存在强大的均衡力量,当情况偏离均衡时会迅速校正,你也可以使用高斯方法。否则,请忘记它。这就是为什么大量经济学研究以均衡概念为基础:别的好处不说,它起码使你能够把经济现象当作高斯变量处理。
但凯特勒把这种思想带入了另一个层面。通过收集统计数据,他开始制造“平均”的标准。胸围、身高、新生儿体重,很少有什么逃过他的标准。他发现,随着对平均值的偏离越来越大,这种偏离的可能性呈指数下降。提出“平均人”的概念之后,凯特勒先生的注意力转向了社会事物。平均人具有他的习惯,按照他的方式消费,使用他的方法。
我已经强调过,有两种不同的随机性,它们具有本质的不同,就像空气与水。一种不关心极端情况,另一种受到极端情况的严重影响;一种不会产生黑天鹅,另一种会。我们不能使用同一种方法讨论气体和液体。即使能,我们也不能把这种方法称为“近似”。一种气体不可能与一种液体“近似”。
通过创造体质平均人和精神平均人,凯特勒创造了偏离平均值的范围,所有人要么在平均值左边,要么在平均值右边,他还对那些站在钟形曲线极左端和极右端的人进行惩罚。这些人成了另类。
传统的高斯方法只关注平均水平,把意外当作附属问题。我们还有另一种方法,它把意外当作起点,把平均水平当作附属问题。
人们应该对凯特勒同时代的科学界给予一定赞誉,他们并没有立即接受他的论点。比如,哲学家、数学家、经济学家奥古斯丁·库诺特(Augustin Cournot)认为不能纯粹基于量化标准创造一个标准人。标准应该取决于相关特性,一个领域的衡量标准区别于另一个领域的衡量标准。应该用哪一个作为标准呢?平均人会是一个怪兽,库诺特说。我将在后面解释他的观点。
我将在此总结并重申本书此前提出的观点。由于钟形曲线的不确定性计量方法忽视了跳跃性或者不连续变化发生的可能性及影响,因此无法适用于极端斯坦。使用它们,就好像只看见小草,而看不见参天大树。虽然发生不可预测的大离差的可能性很小,但我们不能把它们当作意外而置之不理,因为它们的累积影响非常强大。
假设做一个平均人有什么值得向往的话,那一定是具备某种专长,即在这项专长上他比其他人更有天赋——他不可能在一切事情上都是平均的。钢琴家平均来看更擅长弹钢琴,但在骑马方面,则不太擅长。绘图员则更擅长绘图等等。在概念上,平均人与一个在所有方面都平均的人是不同的。实际上,一个绝对平均的人应该一半男一半女。凯特勒完全忽略了这一点。
小草与大树
上帝的失误
请注意,这并非完全来自不确定性。某些情况有80/20的集中度,但同时具有可预测性,这使人们很容易做决策,因为你可以事前确定那重要的20%在哪里。这些情况很容易控制。例如,马尔科姆·格拉德威尔在《纽约客》的一篇文章中写道,对囚犯的大部分虐待行为出自极少数邪恶的狱警。把这些狱警清除掉,虐囚率就会大大下降。(相反,在出版业,你无法事先知道哪本书能赚大钱。战争也是,你无法事先知道哪场战争会威胁大量地球居民。)
更令人担忧的是,在奎特利时代,高斯分布被称为la loi des erreurs,即误差法则,因为其最初的应用是研究天文测量中误差的分布。你同我一样不安吗?对平均值(在这里同时也是中值)的偏离居然被当作误差!
80/20法则只是比喻的说法,它并不是法则,更不是严格的规律。在美国出版业,分配比例更可能是97/20(也就是97%的图书销量来自20%的作者)。如果只看非虚构类作品,情况更严重(8000种图书中的20种占据一半的销量)。
这一概念很快风靡。人们混淆了“应该是”和“是”,而这一点获得了科学界的许可。这一概念浸润在新生的欧洲中产阶级文化中,即后拿破仑时代的商店主文化,受这种文化影响的人们对过度的财富和才华小心翼翼。实际上,对财富扁平化分配社会的梦想符合面临基因博彩的理性人的渴望。如果你必须选择下辈子降生于怎样的社会,但不知道等待你的是什么结果,你很可能选择不冒险。你会希望降生于一个没有贫富差别的社会。
从数学公理上讲,这一法则的表述不一定是最令你吃惊的:它可以很容易地被改称为50/01法则,也就是50%的工作由1%的人完成。它使得世界看上去更加不公平,但这两个法则其实是完全一样的。为什么?假如存在不平均,那么在80/20法则的那20%当中也存在不平均,即少数人完成大多数工作。其最终结果是,大约1%的人完成稍稍超过50%的工作。
赞美平均主义的一个娱乐性结果就是法国一个叫作布德热主义(Poujadism)的政党的诞生,它起初是一场杂货铺运动——一种非无产阶级革命。那些不太被社会眷顾的人互相温暖地拥抱着。数学工具的运用反映出一种杂货铺老板的思想。高斯的数学是为这些商店主提供的吗?
你听说过80/20法则吗?它是一种标志性的幂律,实际上幂律的发现正是从它开始的。当时维尔弗雷多·帕累托观察到意大利80%的土地被20%的人占有。有人运用这一法则指出,80%的工作由20%的人完成;或者80%的工作只产生20%的结果。
彭加莱的救援
极端斯坦与80/20法则
彭加莱本人对高斯方法非常怀疑。我猜当他看到高斯方法及类似的描述不确定性的模型时,会感到忧虑。只要想一想,高斯方法最初是用来衡量天文误差的,而彭加莱关于天体运行机制的思想则包含了更深的不确定性。
为什么会这样?用身高问题对比一下。如果我告诉你两个人的身高加总为4米,你会认为最可能的情况是两人各2米,而不是一人1米,一人3米;甚至也不是一人1.5米,一人2.5米!身高高于2.5米的人几乎没有,所以这种组合不太可能存在。
彭加莱写道,他的一位“杰出的物理学家”朋友向他抱怨,物理学家喜欢使用钟形曲线,因为他们以为数学家认为它是必备的数学工具;而数学家使用钟形曲线,是因为他们以为物理学家认为它是经验事实。
这种倾斜在图书销量中更为明显。如果我告诉你两位作者的书一共销售了100万册,最可能的情况是一位作者的书销售了99.3万册,另一位的销售了7000册。这种情况比每位作者分别销售50万册的可能性大得多。对于大的总数,其构成会越来越不对称。
消除不公平影响
想想下面的例子。从美国人群中随机挑选两个年收入加起来为100万美元的人。他们分别的收入最可能是多少?在平均斯坦,最可能的组合是各50万美元。在极端斯坦,最可能的是5万美元与95万美元。
我在此声明,我是相信中庸和平均主义的价值的。什么样的人道主义者会不想缩小人与人之间的差距呢?没有什么比自私的超级精英思想更令人反感的了!我真正关心的问题是认知上的。现实世界不是平均斯坦,所以我们要学会接受这一点。
让我们更近距离地观察不平均的本质。在高斯框架下,随着离差的扩大,不平均程度降低,因为概率在加速降低。在突破性框架下不是这样:不平均程度保持不变。超级富人中的不平均与中等富人中的不平均程度是一样的,它没有缓和。[6]
“希腊人会把它奉若神明”
不平均
由于钟形曲线具有柏拉图式的纯粹,因此头脑被钟形曲线牢牢占据的人多得令人难以置信。
记住:高斯钟形曲线都受到一种阻力影响,因而偏离平均值的概率下降得越来越快,突破性分布或者曼德尔布罗特分布则不受这种限制。这基本上就是你需要知道的。[5]
查尔斯·达尔文的表弟弗朗西斯·高尔顿(Francis Galton)爵士大概与他表兄一样,是最后的独立绅士科学家之一,这些科学家还包括卡文迪什、开尔文、维特根斯坦因(以他独特的方式)以及我们的大哲学家罗素。虽然凯恩斯不属于这一类,但他的思想在此之列。高尔顿生活在维多利亚时代,当时的世袭贵族和有闲阶层除了骑马和打猎之外,还可以选择成为思想家、科学家或者政治家(对那些天分不高的人来说)。那个时代有许多值得人们向往的东西:纯粹为了科学而从事科学,而不存在直接的职业动机。
记住什么
不幸的是,为了对知识的热爱而从事科学并不一定意味着你会走向正确的方向。一接触并吸收“正态”分布,高尔顿就迷上了它。据说他曾声称,假如希腊人知道它,他们会把它奉若神明。也许正是他的狂热推动了高斯分布的普遍使用。
我想用这些数字定性地说明两类分布的不同。第二种是具有突破性的,它的变化不受阻力影响。请注意,突破性的另一个叫法是幂律。只是知道我们处于一个幂律环境并不能让我们获得很多信息。为什么?因为我们必须计算现实生活中的参数,这比在高斯框架下困难得多。只有高斯分布能够很快显现出特性。我的建议就是只把它当作看待世界的一般方法,而不是精确的解决办法。
高尔顿没有数学天分,但对计量却有少见的热爱。他并不知道大数定理,但自己从数据中发现了它。他造出了梅花相位机,这是一种演示钟形曲线如何形成的弹球机器,我在几个段落以后会讲到它。确实,高尔顿只是在基因和遗传领域应用形曲线,而在这些领域的应用是正确的。但他的狂热帮助这种新生的统计方法进入了社会领域。
高于1600万欧元:……我的任何一台电脑都无法进行这项计算
请回答“是”或“否”
高于800万欧元:16000000000000000000000000000000000分之一
我在这里谈一谈危害的程度。如果你从事的是定性的推理,比如哲学或医学,你需要寻找一些“是”或“否”的答案,而不需要考虑数量的大小,那么你可以假设你处在平均斯坦而不会产生严重的问题。低概率事件的影响不会很大。你要么有癌症,要么没癌症;你要么怀孕了,要么没怀孕,等等。死亡或怀孕的程度并不相关(除非是流行病)。但如果你面对的是合计数字,其大小是重要的,比如收入、财富、投资组合的收益或图书销量,那么使用高斯分布就会有麻烦,因为高斯分布在此不适用。一个数字就能瓦解你的所有平均值,一次亏损就能抹平一个世纪的利润。你再也不能说“这是意外”。“当然,我可能亏钱”再也传递不了任何信息,除非你能对亏损进行量化。你可能亏掉所有净资产,也可能亏掉日均收入的一小部分,这是有区别的。
高于400万欧元:886000000000000000分之一
所以,我在本书较早的章节曾经提到,经验心理学及其对人类本性的研究不受钟形曲线应用的影响。这些研究是幸运的,因为它们的大部分变量可以适用传统的高斯统计方法。在衡量样本中有多少人有心理偏差或犯错误时,这些研究通常只需要回答“是”或“否”。单个观察结果不可能瓦解整体结果。
高于300万欧元:14000000000分之一
下面我将从头开始详细介绍一种独创的钟形曲线表现方法。
高于200万欧元:127000分之一
关于钟形曲线如何形成的想象实验
净资产高于100万欧元:63分之一
请看图15–3所示的弹球机。发射32个球,假设背板足够平衡,每个球在撞到撞针时落到右边和左边的概率相同。你所预期的结果应该是许多球会落入中间的球道,而且离中间球道越远的球道里的球数越少。
高斯分布的财富分配
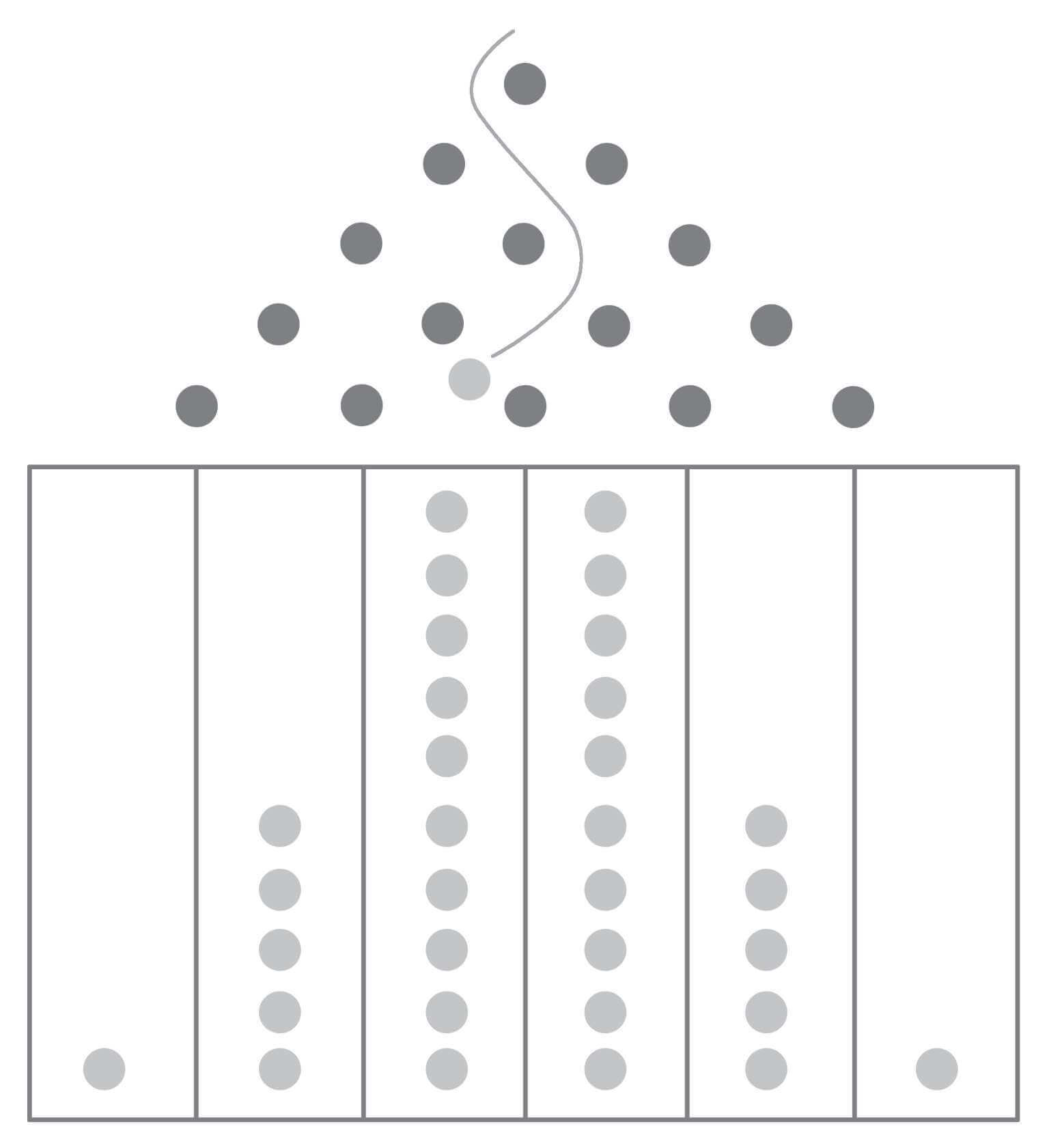
在高斯分布中,我们会看到下面的结果。
图15–3 梅花相位机(简化的)——弹球机
高于64000万欧元:40000分之一
注:释放小球,小球在每个撞针处随机落向左边或右边。图中显示的是最可能的情景,与钟形曲线(高斯分布)极为相似。图片由亚历山大·塔勒布提供。
高于32000万欧元:20000分之一
下面做一个想象实验。一个抛掷硬币的人每抛一次都根据硬币的正反面向左或向右走一步。这叫作随机漫步,但与走路并没什么关系。你可以不向左或向右走,而是赢或输1美元,然后记下口袋里的钱。
高于3200万欧元:2000分之一
假设我让你加入一个(合法)赌局,你要么走好运,要么走背运。抛出硬币,正面,你赢1美元;反面,你输1美元。
高于1600万欧元:1000分之一
抛出第一次,你要么赢要么输。
高于800万欧元:500分之一
抛出第二次,可能结果的数量翻了一倍:情况1:(赢,赢);情况2:(赢,输);情况3:(输,赢);情况4:(输,输)。每种情况概率相同,一次输加一次赢的组合的概率则翻一倍,因为情况2和情况3[(赢,输)和(输,赢)]导致的结果是一样的。这就是高斯分布的关键。中间部分的结果抵消了,而许多情况落入中间。所以,如果每轮赌1美元,两轮以后你赢或输2美元的概率都是25%,但有50%的概率不赢不输。
高于400万欧元:250分之一
我们再来一轮。第三轮可能出现的结果的数量再翻一番,所以我们有8种可能。情况1,在第二轮中的(赢,赢),变为(赢,赢,赢)和(赢,赢,输)。我们在前一轮的每一个结果后面分别加上赢和输,情况2变成(赢,输,赢)和(赢,输,输),情况3变为(输,赢,赢)和(输,赢,输),情况4变为(输,输,赢)和(输,输,输)。
高于200万欧元:125分之一
我们现在有8种情况,每种概率相同。再次注意你可以把一些中间结果放在一起,从而抵消掉一些输和赢。(在高尔顿的梅花相位机中,一只球先落向左边再落向右边或者相反的情况占大多数,所以最后许多球在中间。)净结果或累积结果如下:(1)3次赢;(2)2次赢,1次输,净赢1次;(3)2次赢,1次输,净赢1次;(4)1次赢,2次输,净输1次;(5)2次赢,1次输,净赢1次;(6)2次输,1次赢,净输1次;(7)2次输,1次赢,净输1次;(8)3次输。
净资产高于100万欧元:63分之一
在8种情况中,3次赢出现一次,3次输出现一次,净输1次(1次赢,2次输)出现三次,净赢1次(1次输,2次赢)出现三次。
极不公平的财富分形分布
再来一轮,第四轮,将有16种概率相同的结果。4次赢会出现一次,4次输出现一次,2次赢出现4次,2次输出现4次,不赢不输出现6次。
当然,曼德尔布罗特的极端斯坦可以有多种形式。比如财富极度集中的极端斯坦——如果财富翻番,概率只降低一半。结果在数量上会与上面的例子大不相同,但符合相同的逻辑。
弹子球例子中的梅花相位机(quincunx,名字来源于拉丁语中的5)显示的是第五轮的情况,此时有64种可能的结果,很容易跟踪。以上就是弗朗西斯·高尔顿的梅花相位机背后的原理。高尔顿不够懒惰,而且是一个太天真的数学家。假如不建造这个精巧的装置,他本可以研究更为简单的代数学,或者做一个像这样的想象实验。
回忆一下第三章对突破性和非突破性的比较。突破性意味着不存在使你慢下来的阻力。
我们接着玩。继续抛,直到抛出40次硬币。你可以在几分钟内完成,但我们需要计算器才能算出可能结果的数量,它对我们的简单思维方法而言太困难了。你会有1099511627776种可能的组合,超过1万亿种。不要试图用手算,那是2的40次方,因为每一轮结果翻一倍。(回想一下,我们在第三轮的每一个可能结果后面分别加上赢和输,从而得到第四轮的可能结果,因此可能的结果会翻倍。)这些组合中,40次全是正面只出现一次,40次全是反面也只出现一次。其余的都分布在中间结果附近,也就是不赢不输。
这里概率下降的速度是固定的(或者没有下降)!金额每翻一倍,概率变为原来的1/4,不管金额多大,不管是800万欧元还是1600万欧元。简而言之,这就是平均斯坦和极端斯坦的区别。
我们已经可以看到,在这类随机性中,极端情况极少出现。这超过1万亿种可能中40次全是正面的情况只出现一次。如果你每小时抛40次硬币,连续得到40次正面的概率是如此小,以至于你真要不断地抛才看得到这一结果。假设你不时休息一会儿,去吃东西、与朋友吵架、喝杯啤酒或睡觉,你需要400万辈子才能看到一次40次全正面(或40次全反面)。想一想下面的情况:假设你再加一次,一共41次,要想获得41次全正面将需要800万辈子!从40次到41次,概率降低了一半。这是不具突破性的随机性分析框架的关键特征:出现极端离差的可能性以加速度下降。连续得到50次正面需要40亿辈子!
高于32000万欧元:6400000分之一
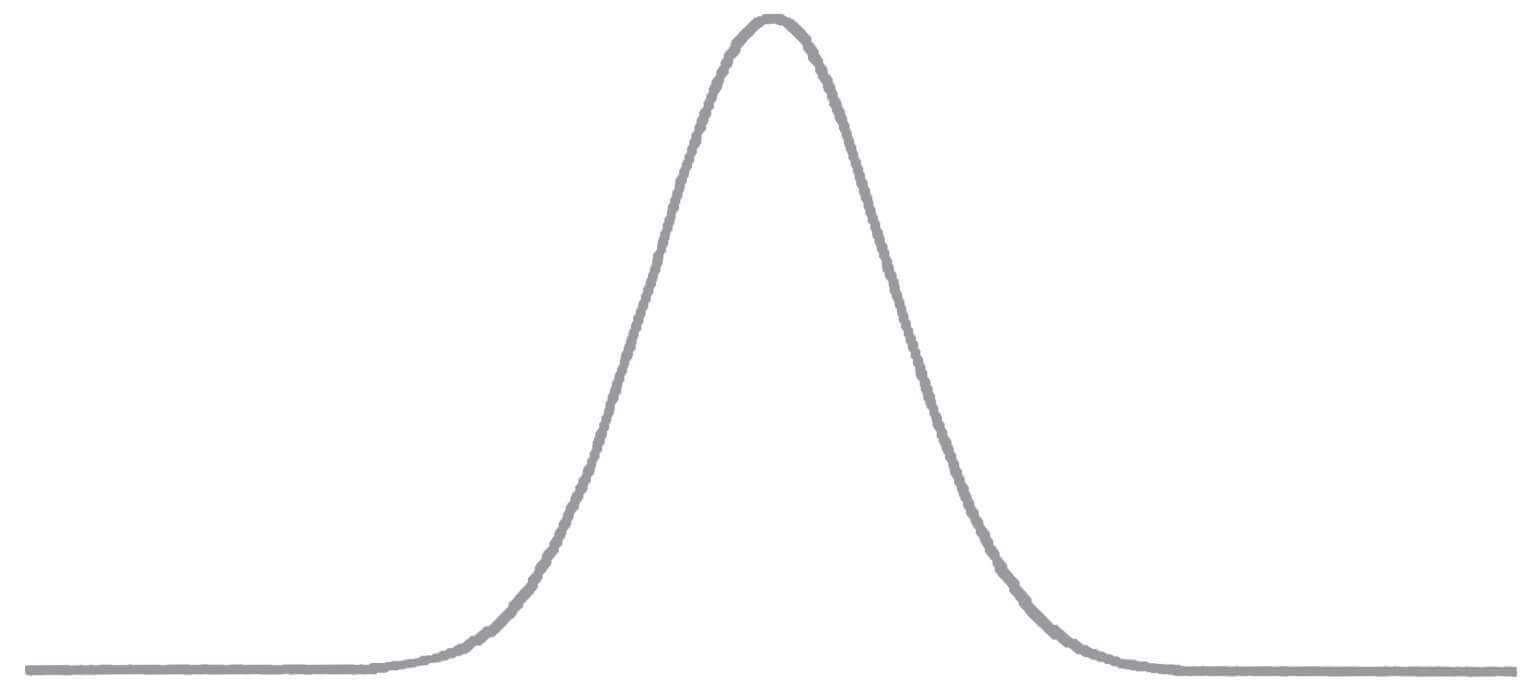
我们还没有完全得到钟形曲线,但已经十分危险地接近了。这只是原始高斯分布,但你已经可以看出关键点了。(实际上,你永远不会遇到纯粹意义上的高斯分布,因为它是一种柏拉图化的形式,你只能接近,但不可能达到。)如图15–4所示,熟悉的钟形已经开始显现了。
高于3200万欧元:64000分之一

高于1600万欧元:16000分之一
图15–4 获得赢面的次数
高于800万欧元:4000分之一
注:抛出硬币40次的结果,原始的钟形曲线形成了。
高于400万欧元:1000分之一
我们怎样才能更接近完美的高斯钟形曲线呢?将抛硬币的过程细化。我们可以抛40次,每次赌1美元,或者抛4000次,每次赌10美分,然后把结果加总。你可能以为两种情况的风险是一样的,但这是假象。两者的等同性之间存在一点反直觉的障碍。赌局次数变为之前的100倍,但赌注变为了1/10,现在不要问原因,只要假设它们是“等同的”。整体风险是等同的,但现在我们有可能连续赢或输400次。概率是大约1后面120个零分之一,也就是1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000次中出现一次。
高于200万欧元:250分之一
再继续这一过程。我们从抛40次,每次赌1美元,到抛4000次,每次赌10美分,再到抛400000次,每次赌1美分,这样我们离高斯分布越来越近了。图15–5显示了–40至40的分布情况,也就是80个绘制点(plot points)之间的分布情况。下一个会达到8000个绘制点。
净资产高于100万欧元:62.5分之一
我们继续。我们可以抛4000次,每次赌1/10美分。如果抛400000次,每次赌1/1000美分呢?作为一种柏拉图化的形式,真正的高斯曲线就是抛无穷次硬币,每次赌无穷小金额的情况。不要试图想象结果,或者试图理解。我们不可能有“无穷小”的赌注(因为如果有,那么我们就处于一个被数学家称为连续框架的事物中),好在我们有替代品。
突破性财富分布
作为比较,下面看看在欧洲成为富人的可能性。假设这里的财富具有突破性,也就是满足曼德尔布罗特分布。(这不是对欧洲财富的准确描述,只是为了简化突出突破性分布的原理。)[4]
图15–5 更抽象的版本:柏拉图的曲线
曼德尔布罗特分布
注:抛无穷次硬币的情况。
这种急剧下降的概率使你能够忽视意外。只有一种曲线能描述这种下降,那就是钟形曲线(以及它的非突破性同胞)。
我们从简单的赌博转入了某种完全抽象的东西,从普通观察走进了数学的领地。在数学中,事物都有一种纯粹性。
我列出一系列数字的目的在于表现出加速。看看比平均值分别高出60厘米和70厘米的情形:只增加了10厘米,可能性就从10亿分之一变为7800亿分之一!从70厘米增加到80厘米时,可能性就从7800亿分之一变成1600万亿分之一![3]
现在,我要说明完全抽象的东西是不存在的,所以请不要试图理解图15–5,只要知道它的用处就行了。把它当作温度计:你不明白温度是什么意思也可以谈论它。你只需要知道温度与舒适度(或其他实际考虑)的关系。你不需要关心能够从更专业的角度解释温度的粒子间的碰撞速度。温度,从某种意义上说,是你的大脑将某种外部现象转化为数字的方式。同样,高斯钟形曲线就是使得观察值落入一个正负标准差之间的概率为68.2%的分布。我重复一次:不要试图理解标准差是不是平均偏差——不是,而许多(太多了)使用标准差这一说法的人不明白这一点。标准差只是一个参照数字,只是一种对应性,如果相关现象是高斯现象的话。
我相信,在22个偏离单位之后,也就是比平均值高出220厘米,可能性会变为一个古戈尔分之一(古戈尔是1后面加100个零)。
标准差经常被称为西格玛。人们还会谈论“方差”(方差是西格玛,也就是标准差的平方)。
比平均值高110厘米(高于2.77米):36000000000000000000000000000000000000000000000000000000000000000000000000000000000000000分之一
请注意曲线的对称性。不论西格玛是正是负,结果都是一样的。小于–4西格玛的概率与大于4西格玛的概率是一样的,在这里是32000分之一。
比平均值高100厘米(高于2.67米):130000000000000000000000分之一
读者可以看到,高斯钟形曲线的关键点在于大部分观察值集中在平均水平附近,也就是平均值,随着对平均值的偏离越来越大,偏离发生的可能性下降得越来越快(呈指数下降)。如果你需要记住一点,那么请只记住偏离平均值时可能性下降的速度。意外变得越来越不可能发生,你可以安全地忽略它们。
比平均值高90厘米(高于2.57米):8900000000000000000分之一
这一特性同样产生了平均斯坦的最高法则:鉴于较大离差的稀少性,它们对总体的影响小到可以忽略不计。
比平均值高80厘米(高于2.47米):1600000000000000分之一
在本章较早部分关于身高的例子中,我以10厘米为偏离单位,展示了随着高度的增加,偏离发生可能性的降低。这些是1西格玛的偏差,身高表还提供了以西格玛为计量单位的“西格玛尺度”的例子。
比平均值高70厘米(高于2.37米):780000000000分之一
方便的假设
比平均值高60厘米(高于2.27米):1000000000分之一
请注意我们在带来原始高斯分布或温和随机性的抛硬币游戏中的核心假设。
比平均值高50厘米(高于2.17米):3500000分之一
第一核心假设:每次抛硬币是独立的。硬币没有记忆。前一次得到正面或反面不会影响下一次得到正面或反面的概率。你不会随着时间的推移变成“更好”的抛硬币手。如果考虑记忆,或者抛硬币的技巧,整个高斯世界都会动摇。
比平均值高40厘米(高于2.07米):32000分之一
回忆我们在第十四章中谈到的偏好依附和累积优势。两种理论都假设今天的成功会增加你在未来成功的可能性。因此,概率取决于历史,高斯钟形曲线的第一核心假设在现实中不成立。当然,在游戏中,过去的胜利不会意味着未来胜率的提高,但现实生活中不是这样,这就是我对从游戏中学习概率感到担忧的原因。但当胜利带来更多胜利时,与原始高斯曲线的情况相比,你更有可能看到连赢40次的结果。
比平均值高30厘米(高于1.97米):740分之一
第二核心假设:没有“疯狂”的跳跃。比如,我们随机步行的步长总是已知的,步长不存在不确定性。我们不会遇到步长剧烈变化的情况。
比平均值高20厘米(高于1.87米):44分之一
请记住,假如这两条核心假设中有任何一条不满足,你的步骤(比如抛硬币)的累积结果就不会得到钟形曲线。视实际情况,它们可能导致曼德尔布罗特式的幅度不变的疯狂随机性。
比平均值高10厘米(高于1.77米):6.3分之一
“高斯分布无处不在”
高斯的主要理论是,大部分观察结果集中在中等水平附近,也就是平均值附近;随着对平均值的远离,偏离平均值的可能性下降得越来越快(呈指数下降)。假如必须以一句话来表示这一理论,那就是:离中心(也就是平均值)越远,可能性的下降速度便越快。下面的数字显示了这一点。我以一个高斯变量为例,例如身高(对它做了简化,使演示更清楚),假设平均身高(男人及女人)是1.67米。我把一个偏离单位定义为10厘米。然后我们在1.67米之上逐渐增加高度,并考虑人们身高为这个高度的可能性。[2]
我在现实中遇到的一个问题是,每当我告诉人们高斯钟形曲线在实际生活中并不普遍存在,而只存在于统计学家的头脑中时,他们就会要求我“证明”这一点。这很容易,在后两章我们会看到,但没人能够证明相反的观点。每当我举出一个不是高斯分布的例子,人们就会问我这样做有什么合理性,并且要求我“给出现象背后的理论”。我们在第十一章看到了一个富者更富的模型,它可以说明为什么不应使用高斯分布。模型的构想者不得不浪费时间写关于哪些模型可以产生突破性分布的理论,似乎他们必须为此道歉一样。理论!我对这一点有一个认知上的问题,我不明白为什么我们要为世界不能满足某个理想模型找理由,而这个模型只不过是得到了对现实视而不见的人的追捧。
减少中的增加
我的做法不是研究哪些模型会产生非钟形曲线的随机现象,因为这样做会犯和盲目理论化一样的错误;相反,我尽可能深入地理解钟形曲线,以确定它在哪里适用,在哪里不适用。我知道平均斯坦在哪里。在我看来,经常是(不,几乎一直是)那些使用钟形曲线的人不懂得钟形曲线,因此不得不对其进行合理化。
注:上面印着高斯的头像,他的左边是平均斯坦的钟形曲线。
世界并不存在高斯分布的普遍性,它只是一个思维问题,产生于我们认识世界的方式。
图15–1 最后的10德国马克纸币
下一章将讨论自然的尺度不变性,以及分形现象的特点。再下一章将探讨高斯分布在社会经济生活中的错误应用以及“制造理论的需要”。

我有时有一点情绪化,因为我花了大量时间思考这个问题。自我开始思考并且进行大量想象实验以来,还从来没有在商业界和统计界碰到过一个能够既接受黑天鹅思想又抛弃高斯和高斯方法的人。许多人接受我的黑天鹅思想,但无法把它贯彻到最后的结论,也就是你不可能只使用一种叫作标准差(还称之为“风险”)的东西衡量随机性;你不能期待对不确定性的特点做简单总结。要把黑天鹅思想贯彻到底,你需要勇气、努力、透过现象看本质的能力以及彻底理解随机性的愿望。它还需要你不把别人的观点奉若神明。我还发现一些物理学家抛弃了高斯方法,却落入另一个错误:对精确预测模型的轻信,主要是第十四章所讨论的偏好依附——又一种形式的柏拉图化。我无法找到一个有深刻的洞察力和科学技能、把数学当作辅助工具而不是主要目的的人。我花了近15年时间才找到另一位思想家,他把许多天鹅变成了灰色,这个人就是曼德尔布罗特——伟大的贝诺特·曼德尔布罗特。
真是令人震惊,钟形曲线竟然成为风险管理工具,被监管者和穿深色西服、以乏味的方式谈论货币的中央银行人员使用。
[1] 本章详细讨论钟形曲线,非专业(或直觉不强的)读者可以跳过这一章。或者,假如你是一个不知道钟形曲线的幸运者,也可以跳过这一章。
这是极度的讽刺,因为与德国货币最不相关的就是这一曲线:马克与美元汇率在20世纪20年代的短短几年间从1美元兑换4马克变为1美元兑换4万亿马克,这说明钟形曲线在描述汇率变动的随机性时毫无意义。只需要出现一次这种情况就能让你抛弃钟形曲线——只要一次,你只需要想一想它的后果。但这张纸币上印着钟形曲线,旁边是高斯博士,他长相平庸,看上去有一点严厉,显然不是我想与之在阳台上一起消磨时光、喝茴香酒、漫无边际地闲聊的那一类人。
[2] 为了简便,我对数字进行了一点编造。
我在机场有足够的空闲时间,这是我尝一尝欧洲黑巧克力的大好机会,尤其是我成功地说服自己在机场消费的卡路里是不算数的。收银员找给我一张10德国马克的纸币。德国马克不久后就会退出流通,因为欧洲将改用欧元。我把它作为一种告别纪念保留。欧元诞生之前,欧洲有许多种货币,这对印刷商、货币兑换商,当然还有我这样的外汇交易商来说是好事。当我吃着我的欧洲黑巧克力,若有所思地看着这张纸币时,差一点噎着。我突然发现,而且首次发现,它上面有一样很有意思的东西。这张纸币上印着高斯的头像以及他的高斯钟形曲线。
[3] 高斯分布最容易产生错误理解的地方,在于它在尾部事件估计上的脆弱和不足。4西格玛的概率是4.15西格玛的两倍。20西格玛的概率是21西格玛的1万亿倍!也就是说,西格玛值的一个微小差错将导致对概率的极大低估。对于某些事件,我们的错误可以达到上万亿倍。
2001年12月,我从奥斯陆去苏黎世,在法兰克福机场转机。
[4] 我在整个第三部分将以一种或另一种形式表达的主要观点如下:当你假设有且只有两种可能的例子时,一切在观念上都变得简单——不具突破性的(比如高斯分布)和其他(比如曼德尔布罗特随机性)。我们之后会看到,抛弃对不具突破性的理论的应用足以消除对世界的某些想象。这就像负面经验主义:通过确定什么是错的来获得知识。
高斯与曼德尔布罗特
[5] 请注意,变量不一定具有无限的突破性;可能存在一个非常遥远的上限,但我们不知道具体在哪里,所以我们把具体情况当作具有无限突破性。技术上讲,一本书的销量不可能超过地球上的居民数量,但这种上限已经大到可以被认为不存在。而且,重新包装一下,这些书或许能够卖给同一个人第二次,谁知道呢。
忘掉你在大学听过的一切统计学或概率理论吧。假如你没上过这类课,那更好。让我们从头说起。
[6] 2006年8月我修改本书时住在马萨诸塞州戴达姆市的一家酒店,这家酒店位于我小时候参加过的一个暑期夏令营附近。在那里,我有点惊异地看到许多有体重问题的人,他们在大厅里走来走去,还造成电梯堵塞。后来我发现美国肥胖接纳协会(National Association of Fat Acceptance)的年会正在那里召开。由于大部分成员都极为肥胖,我无法辨认哪个代表体重最重:在这个极度肥胖的人群中存在某种公平(比我看到的这些人还要胖得多的人已经死了)。我相信,在美国富人接纳协会的年会上,会有一个富人让其他人都相形见绌,即使在超级富人当中,也会有一小部分人占有总体财富的大部分。
由于钟形曲线的不确定性计量方法忽视了跳跃性或者不连续变化发生的可能性及影响,因此无法适用于极端斯坦。使用它们,就好像只看见小草,而看不见参天大树。虽然发生不可预测的大离差的可能性很小,但我们不能把它们当作意外而置之不理,因为它们的累积影响非常强大。
